
If the data type of the categorical predictor isĬategorical, then you can check the order of categoriesĬategories by using reordercats to customize the Reference level, so it does not include the indicator variable for the reference (categories) includes L – 1 indicator variables. M-estimation to formulate estimating equations and solves them using the method of Iteratively Reweighted Least Squares (IRLS).Ī model with a categorical predictor that has L levels
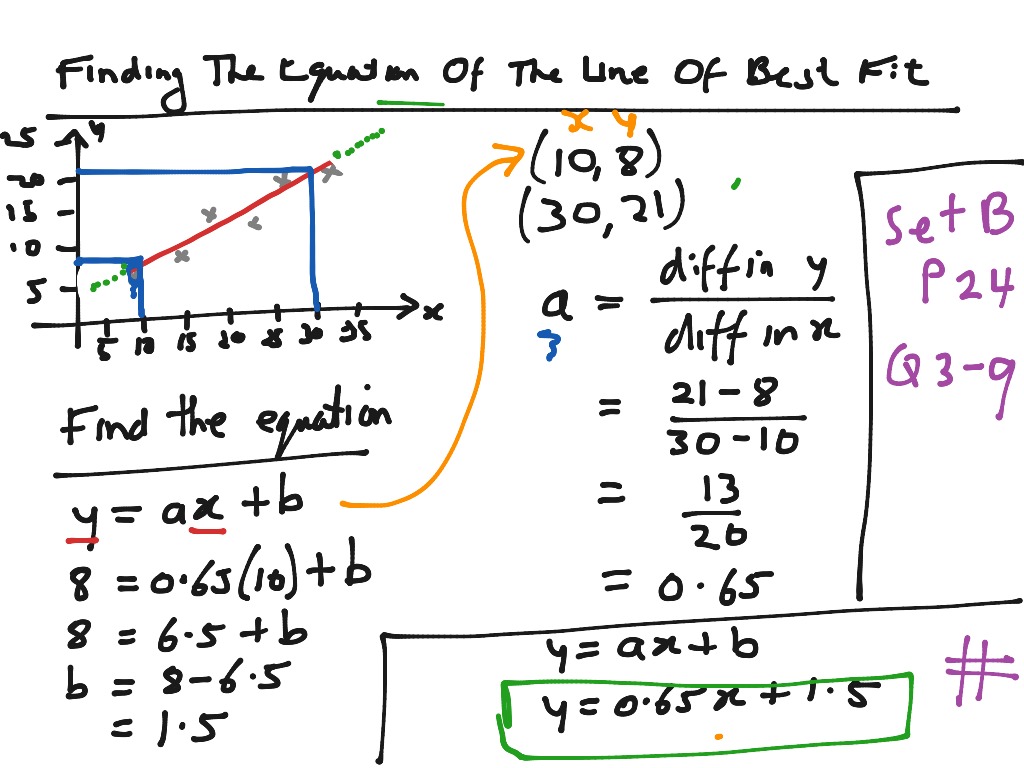
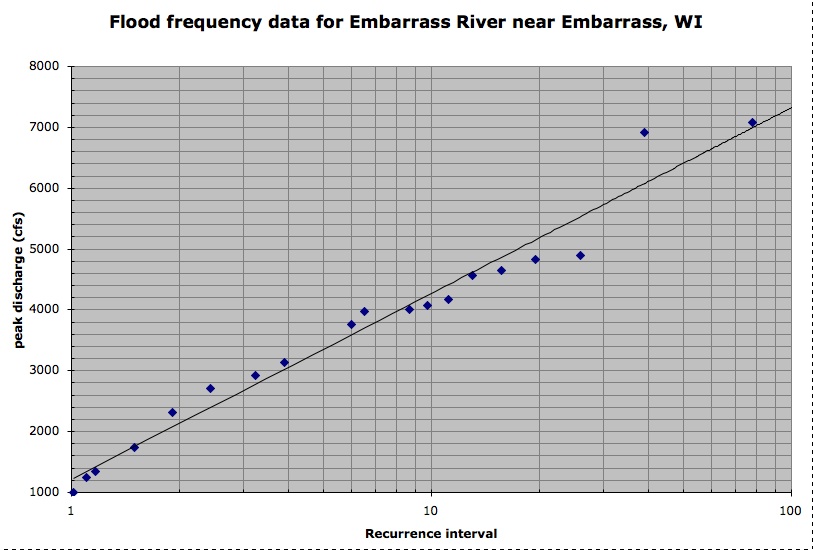
Line best fit scidavis software#
P columns, the software excludes the smallest MAD is the median absolute deviation of the Standard deviation of the error term given by Least-squares fit, and s is an estimate of the H is the vector of leverage values from a Previous iteration, tune is the tuning constant, Where resid is the vector of residuals from the Increasing the tuning constant decreases the downweight assigned to Decreasing the tuningĬonstant increases the downweight assigned to large residuals Has a normal distribution with no outliers. The default tuning constants of built-in weight functions giveĬoefficient estimates that are approximately 95% as statisticallyĮfficient as the ordinary least-squares estimates, provided the response Matrix is convenient when the number of predictors is large and you want to generateĪ character vector or string scalar Formula in the form Number of predictor variables, and +1 accounts for the response variable. Where t is the number of terms and p is the For example,Ī t-by-( p + 1) matrix, or a Terms Matrix, specifying terms in the model, The model contains interaction terms, but the degree of each interaction termĭoes not exceed the maximum value of the specified degrees. Specify the maximum degree for each predictor by using numerals 0 though 9. Predictor, degree j in the second predictor, and so Model is a polynomial with all terms up to degree i in the first Products of pairs of distinct predictors. Model contains an intercept term, linear and squared terms for each predictor, and all Model contains an intercept term and linear and squared terms for each predictor. Model contains an intercept, linear term for each predictor, and all products of pairs of Model contains an intercept and linear term for each predictor. Model contains only a constant (intercept) term. Use the 'components'(default) option to return a component ANOVA table that includes ANOVA statistics for each variable in the model except the constant term. To examine the categorical variable Model_Year as a group of indicator variables, use anova. Each p-value examines each indicator variable. The model display of mdl2 includes a p-value of each term to test whether or not the corresponding coefficient is equal to zero. Mdl2 uses '76' as a reference level and includes two indicator variables Ι Year = 70 and Ι Year = 82. R-squared: 0.531, Adjusted R-Squared: 0.521į-statistic vs. Number of observations: 94, Error degrees of freedom: 91 You can find these statistics in the model properties ( NumObservations, DFE, RMSE, and Rsquared) and by using the anova function. For example, the model is significant with a p-value of 7.3816e-27. P-value - p-value for the F-test on the model. constant model - Test statistic for the F-test on the regression model, which tests whether the model fits significantly better than a degenerate model consisting of only a constant term. For example, the R-squared value suggests that the model explains approximately 75% of the variability in the response variable MPG.į-statistic vs. R-squared and Adjusted R-squared - Coefficient of determination and adjusted coefficient of determination, respectively. Root mean squared error - Square root of the mean squared error, which estimates the standard deviation of the error distribution. For example, the model has four predictors, so the Error degrees of freedom is 93 – 4 = 89. For example, Number of observations is 93 because the MPG data vector has six NaN values and the Horsepower data vector has one NaN value for a different observation, where the number of rows in X and MPG is 100.Įrror degrees of freedom - n – p, where n is the number of observations, and p is the number of coefficients in the model, including the intercept. Number of observations - Number of rows without any NaN values. Compute Mean Absolute Error Using Cross-Validation.Specify Response and Predictor Variables for Linear Model.Linear Regression with Categorical Predictor.Fit Linear Regression Using Terms Matrix.




 0 kommentar(er)
0 kommentar(er)
